Introduction
All decision tasks (questions with Yes-No answers) can be framed as optimisation tasks (minimum quantity for Yes), and as such, any problem can be considered the optimisation of some quantity. It’s an attractive, though mostly useless framework, as optimisation tasks are much harder to solve. Yet somehow we’re in a position, with advances in machine learning, where we have effective computational methods for optimisation. Thus problems in physics, anthropology and economics can be reframed as optimisations and with enough compute, could be replicated. Do I recommend we do this? Hell no. But if we want to create intelligent agents, it’s worth looking at what processes led to the most intelligent agents we know, humans.
Before we start, we should clarify some terms. An optimisation is an abstraction for finding the “best” of something. It has 3 prerequisites; a system, a set of configurations and an objective. In general an optimiser finds the configurations of the system such that it best fits the quantity (objective). Below we set some ground rules:
-
The system must be fixed/stable, this stops configurations or objectives changing as we talk about them or their values being distorted. We call this “closed” to show that nothing can enter or leave it (e.g resources or information).
-
Configurations can either be expressed as all the possible ways to organise a system (think outcomes of a dice roll) or can be described through their degrees of freedom. For example, degrees of freedom could be as simple as positions of a ball in a box (2 degrees of freedom with X and Y coordinate) to the values of the weights of a neural network (which can be over a billion parameters).
-
Objectives can be vague but normally we want to be able to tell when our configuration is better or worse than another configuration (for the given objective). Mathematically, we’d at least like a partial ordering (so we can use $\geq$).
In this work, I’ll go through epochs of history, in which there existed a different predominant optimiser. For structure I’ve listed these epochs below.
Table of Contents
- Start/Nothing
- Entropy/Sampling
- Replicators/Evolution
- Markets/Pareto Improvements
- Agents/BackProp
- Looking Forward
In general, history is terrible at making future predictions, so take this work with a pinch of salt.
Start/Nothing
13.7 Billion Years (+1*10^-43 Sec) Ago
Something happens, nobody is quite sure when, but all we know is now we’ve got lots of energy in a tiny universe, and then suddenly there is a huge universe with plenty of space and time. At this very moment you can’t really apply optimisers, you’re looking at the most incredible dynamic system in our Universe’s history. Thankfully this all calms down in less than 10^-43 of a second. Phew.
Entropy/Sampling
13.7 Billion - 4.3 Billion Years Ago
As everything is pushed away from everything else, it begins to cool and matter comes into existence. Most importantly it doesn’t cool down uniformly, there is more stuff in some places than in others. Heavier quarks and leptons begin to decay. In their place, where pairs existed, neutrons and protons are beginning to form.
In a general sense, we now have today’s universe and we have an infinite number of configurations for how matter is organised in this space. So where’s the optimisation? For the next 10 billion years (or so), the optimisation is governed (more or less exclusively) by the second law of thermodynamics, where the total entropy of an isolated system can never decrease over time. This introduces our metric: entropy.
What is entropy?
Entropy as an equation is seemingly simple but doesn’t explain much. A much better intuition was shared by Alessio Serafini and went something like this: Firstly let’s talk about comparative measurements (absolute references are rare) and let’s look at my desk at two different times. I only place pens and paper on my desk and we can distinguish between them, but not amongst them (all pens look like all other pens).
Desk 1 is exceptionally well organised, my pen pot is always in the top left corner 1cm from the edge, and my papers and pens are meticulously laid out in order, if I were to move a single pen and replace it with paper, you’d notice the state has changed.
Now let’s look at Desk 2, it’s a mess. I have a cluster of pens and pencils around my desk. Some paper is on top of pens and vice-versa. Let’s do the same swap of a pen with paper. Would you be able to notice? Without better organisation you probably wouldn’t notice the state has changed.
Note that Desk 1 and Desk 2 are the same system and we have the same precision in both scenarios, what’s different is that Desk 2 has significantly higher disorder than Desk 1. Thus we say Desk 2 has a higher entropy compared to Desk 1. So entropy becomes this measure of ways we can internally swap things but keep the same outward appearance.
If you’re interested in more Entropy fun, there’s an excellent lecture series on understanding the rich connections entropy can make.
Randomly try everything
But how does this apply in the general world - where is the entropy change in my day to day experiences? When I drop a pen, why does it end up on the ground? Why do atoms form covalent bonds and why does temperature spread out?
In all the above cases, we’re still maximising entropy, but we’re using a cheeky equation which links to free energy. The Gibbs free energy is given by $G = H − TS$, where $H$ is the Enthalpy, $T$ is the absolute temperature, and $S$ is the entropy. Don’t worry about Enthalpy - it’s some strange energy unit which chemists care about (and when the state doesn’t change). The most important takeaway is that (for fixed temperature) as Free Energy gets smaller, Entropy gets bigger.
Most of classical physics focuses on explaining actions through the lens of minimising free energy. Let’s re-evaluate the scenarios from before. When I drop a pen, the pen wants to be in the lowest free energy state possible, so it minimises its gravitational potential energy. When atoms form covalent bonds, electrons are being shared to minimise the total free energy of the combined system (of both individual atoms), which is different to minimising the free energy of two separate systems.
So how does the optimisation take place? How do we end up in these optimal configurations? To glean an answer to this, it makes sense to look at our final question. Why does temperature disperse?
Let’s imagine we have a box of indistinguishable particles, at temperature T, each with their own velocity, and the speed of a randomly selected particle defines the configuration. Then we can describe a (Boltzmann) distribution over all possible configurations with a specific probabilistic weight, given by the Boltzman factor:
$$p_i \propto e^{-\frac{e_i}{\kappa T}}$$
This particular distribution (for velocities of particles in a gas) is called the Maxwell-Boltzmann Distribution. When we want to measure the state, we are simply sampling from an equivalent distribution. Thus the optimisation necessarily is random, it’s pretty much up to chance what velocity we find particles in.
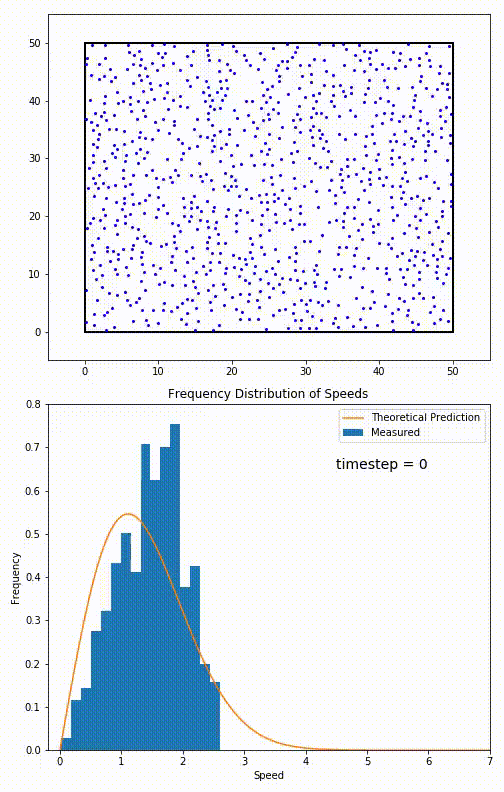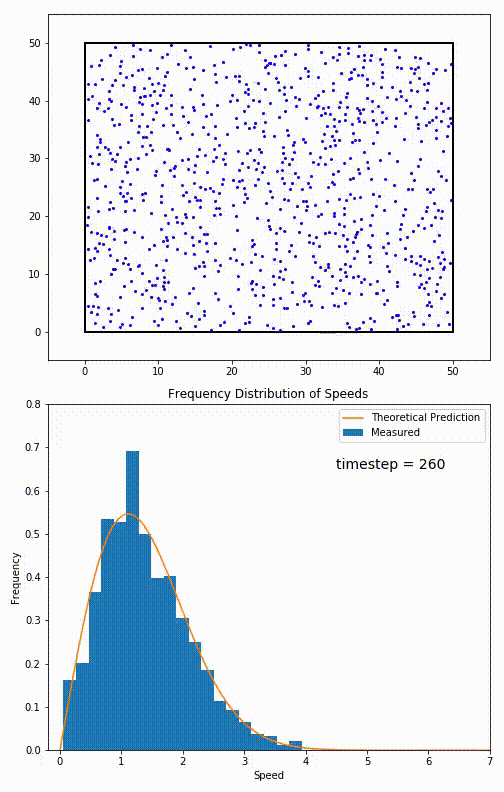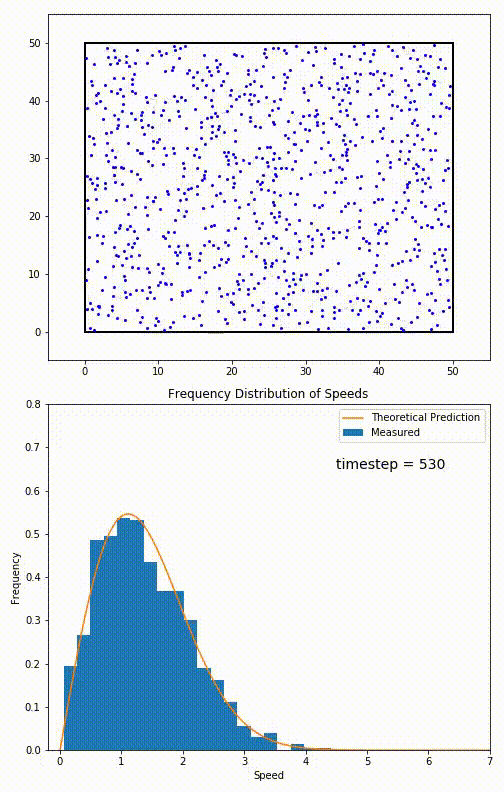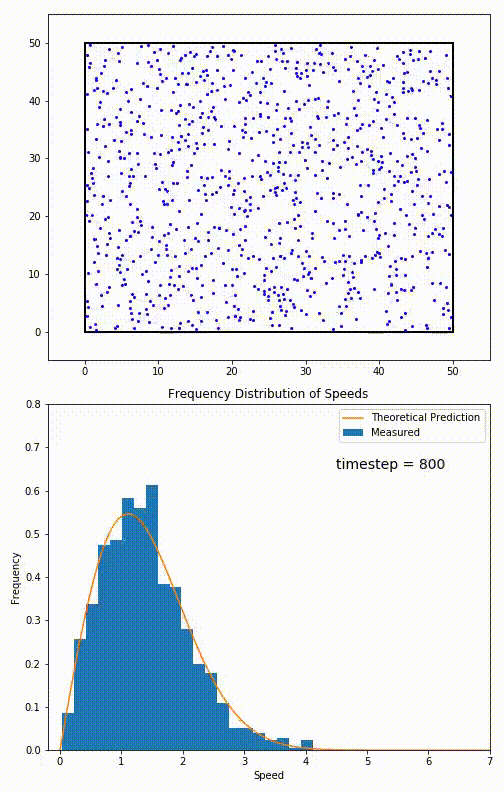
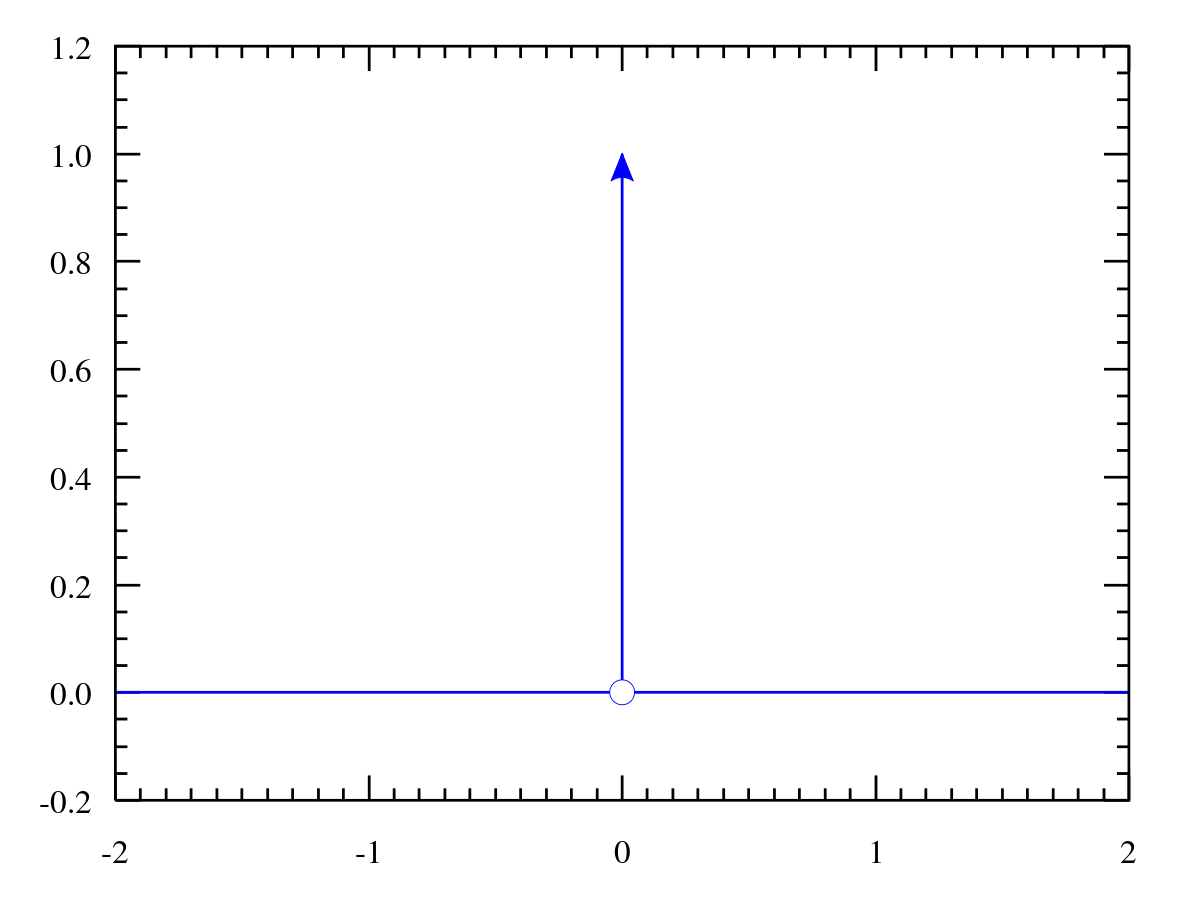
But wait you might be going “But Akbir, my bedroom doesn’t randomly sample everytime I look for where my chair is!” And you’re right, when looking at macroscopic properties (chair location), we end up taking the Thermodynamic Limit:
$$N \to \infty, V \to \infty, \frac{N}{V} = constant$$
This transforms our nice distributions into sharp dirac-delta distributions where any sample we take ends up in a single position.
But what about at the quantum scale? It turns out when you sample from a distribution (take a measurement), the state can collapse (transform) into another distribution or a fixed state (called an Eigenstate). So for physics, optimisation involves randomly sampling from a system until it eventually keeps giving the same answer (it has fallen into eigenstates which relate to high entropy). We can consider this a positive feedback loop - once you’ve collapsed into a fixed state, you continue to stay within it.
So the optimisation technique really isn’t that impressive, physics seems to randomly sample a distribution when not in a thermodynamic limit and in the larger scale it’s boringly always in the correct state. What’s impressive is that entropy optimisation occurs over such a large configuration space, with over $10^{82}$ observable atoms in the universe, assuming we can only permute where these atoms, that’s a whopping $10^{10^{85}}$ states. And most importantly this can be applied at almost any scale of physics, explaining grand structures such as galaxies and planets and also at the molecular level through the van der Waals forces.
Replicators/Evolution
4.3 Billion Years Ago - 300,000 BCE
At some point molecules become larger nucleotides and then RNA molecules. These molecules are able to replicate themselves. Replication increases entropy as it’s a non-reversible process. It’s nothing particularly new, it existed for ages in crystalline structures (see Vonnegut’s Ice 9 for a humorous take on this). What’s interesting is that the features of RNA are dependent on the arrangement of its nitrogenous bases (ACGU) bases.
Here we see our first optimiser handover, from entropy to replication. Firstly our system zooms in from the “Universe” to just “Earth” (as far as we know). Earth is finite, with fixed space and resources. Secondly, the arrangement of nitrogenous base, which provide a replicator its features, become the set of configurations. Optimisation is driven by the fact that replicators must compete for fixed resources. In a finite system, with two replicators $r_1$ and $r_2$, depending on which replicator is more suited to the environment, it will survive/replicate more (reducing resources for others). Thus whoever survives to replicate the most is the best suited configuration ($r_1$ and $r_2$). Importantly, if we consider the larger system again (which includes the big ol’ Sun) then entropy maximisation is still happening.
This is your standard theory of evolution - Generally, we have a generation at time $G_t$, which contains copies (with variation) related to who was most successful in $G_{t-1}$. The most successful members of generation $G_{t}$, then make copies of themselves for $G_{t+1}$. And so at each generation we apply a local random transformation (offspring + variation) and an optimisation (of picking the best genes in the current population) and then over time we move towards the best overall gene (although isn’t guaranteed). For an excellent visualisation of genetic algorithms and when they go wrong check out Hardmaru’s blog.
Gene evolution is already well understood so let’s keep this brief. Systems are agents within an interactive world, configurations (for an agent) are stored in its DNA, and the objective is to replicate the most. However one key component to notice is the optimisation takes at least 1 generation to create new variations and successful genes can take hundreds of years to be passed onto the entire population. Alas, at least unlike entropy optimisation, over time we get closer and closer to the correct answer. Also unlike entropy optimisation, there is flexibility in the objective of replication, the definition of fitness can change over time, whilst entropy can not.
Adding Spice to Optimisation
300,000 - 3000 BCE
Some of these gene replicators eventually grow into homo sapiens, whose collective information, which is passed from generation to generation, becomes an even more interesting replicator - Culture.
Culture is all the information you’ve learnt from others, as opposed to the instinct you were born with. Other animals have this too, but what makes homo sapiens so interesting is how quickly their culture grew. These pesky bipedal hominids spent so much time on the ground, pair bonding and competing against one another, that culture became an important tool for survival. I’m not (necessarily) talking about artsy pictures; more devising tools for fighting and watching other sapiens’ gaze to predict attention. It was culture which helped differentiate which sapiens survived and expanded into new environments. We can consider single units of cultural replicators as memes - think memes/culture as equivalent to genes/phenotype. An example of culture is spice, whilst a meme may be crushing up peppers and adding before cooking. We can even go as far as considering optimising culture as “memetic” evolution.
Let’s examine spice further. Other animals do not spice their food, it provides little nutrition and the active ingredients are aversive chemicals that evolved to keep insects, fungi and animals away from them. Furthermore, humans aren’t born liking spice. Yet our cooking seems to optimise for effective spice use (heat resistant spices such as garlic and onions are used during cooking whilst cilantro is applied fresh). So how did it end up in our food?
The answer is that spice has antimicrobial properties, which reduce the risk of pathogens from foods (especially meat). So it’s clear that at some point, our ancestors chose to augment recipes by adding spice and noticed less people died. They tinkered away, generation by generation, until we got to our amazing recipes now.
But why do we end up liking spice? Let’s look at peppers and the chemical agent Capsaicin, which fires pain receptors in our body. Children from warmer climates (where meat contamination is more likely) have learnt Capsaicin to not only fire their pain receptors but also release dopamine. This learned behaviour - stems from copying other people. Coming from an South Asian culture, spice tolerance was a mark of adulthood amongst my family. Spice demonstrates how culture shapes our biology.

But what does it mean to be successful? In the example of genes it’s the fitness of the environment, but for culture, the environment doesn’t choose what survives, the next generation does. Interestingly humans, who are no smarter than their ape counterparts, are significantly better imitators. In particular, children have been shown not only to be innately better at copying, but also at choosing whom to copy from. Children are great at using three main proxies for finding the best individuals to copy from: Skill (how an individual performs), Prestige (how others perceive the individual) and Self-Similarity (Age and Ethnicity). Note also, it’s not actually the best recipe that is copied, but the most liked chief whose recipes are copied.
All memes aren’t good just as cancerous genes are harmful, for example consider suicide. After the suicide of a high profile individual (with media coverage), we generally see an uptick in the number of suicides committed; it’s a contagious idea. Even more interestingly, suicide didn’t encourage people who “were going to anyway” as the number of suicides returns to the average before the high profile case (otherwise we’d expect to see a drop in the number of suicides after the period of “popularity”). The idea of suicide is attractive and contagious to people. The speed of cultural optimisation is significantly quicker than it’s gene counterpart - with population updates no longer taking entire generations but mere seconds, as new memes are generated instantaneously. For cool examples of how we should prepare against bad memes check out Nick Bostrom’s post on infohazards.
So what cool ideas have memes spread? Firstly through culture evolution we’ve devised languages - efficient mechanisms to convey information from people to people. Language is fantastic, allowing us to create even more culture, as the bandwidth of knowledge we can transmit increases. This is yet another example of how optimisers successfully improve themselves. Culture doesn’t just affect our biology, it also alters our gene evolution. Take our facial muscles, which are significantly weaker than our ape counterparts. Facial muscles were a necessity for breaking down hard foods yet energy expensive. As we learnt to use tools to ground and crush foods, the selection pressures for strong facial muscles reduced and the related genes became unfavourable. Note that culture is changing what genes best fit an environment - with tools we change what environments we are restricted to, freeing up gene evolution. This is aptly named Gene-Culture coevolution and this is what makes humans intelligent - no other species can grow a culture like ours.
So, is cultural evolution an inner optimisation loop of genetic evolution? Both optimisations work with replicators and genetic algorithms, it’s even fair to say without genes, culture would not exist. The important factor to realise is that we’re seeing another optimiser handover - this time from optimisation of genes to optimisation of culture. Note that this doesn’t mean genes don’t continue to be optimised, but they are no longer the dominant force of change! Just like our face muscles, gene-culture coevolution has also reduced our testosterone levels and the need for aggressive conflict. This urshed in an age of self-domestication and large scale cooperation. We’ve learnt that working together is more effective and large societies have started to emerge.
This began a transition away from hunter-gatherers to an agricultural society. Sapiens decided to specialise in single disciplines and trade their skills amongst themselves. To trade they developed currencies, a fungible object which signified value. This required immense trust in the abstract system - a stage only possible, now cultural evolution had shaped humanity.
Markets/Pareto Improvements
3000 BCE - 2020 AD
Sapiens got really good at taking stuff and making more of it. We even gave the extra stuff we make a name - gross produce. This originally was our ability to make more food than needed, so think the number of apples you need to eat to cultivate an orchard of apples. The surplus didn’t go to waste, it actually allowed the populations to grow, and thus make even more food (again another positive feedback loop for an optimiser).
Markets fixed a problem we didn’t even realise we had: some people have more resources than they can use and some people really didn’t have enough. Why? Because our gene optimisation made us want to hoard so badly. And by resources here, I’m considering land, equipment and even people to work on it!
There’s a finite amount of input resources at any point, and there’s a finite number of workers. Let’s assume each worker has their own efficiency, which is a function of the resources you give them (I may be really good at making a single chair but panic if you rush me and ask for 10). Now if I had 1 single worker - I’d simply give all my resources to them and get the most I can back, but if I have 2 workers? Then I need to give them resources accordingly.
In the ideal situation with a fixed output and equally efficient workers, we should share the inputs equally. But in the situation where worker 1 is twice as efficient as worker 2, I should probably give more input resources to worker 2. What we want is for resource allocation to be Pareto optimal. This is just econ chat for saying - there exists no changes that could improve the output without reducing other variables. The optima isn’t unique, as we can imagine two completely different scenarios where the overall output is consistent - below is the equal efficiency case for worker 1 (X) and worker 2 (Y).
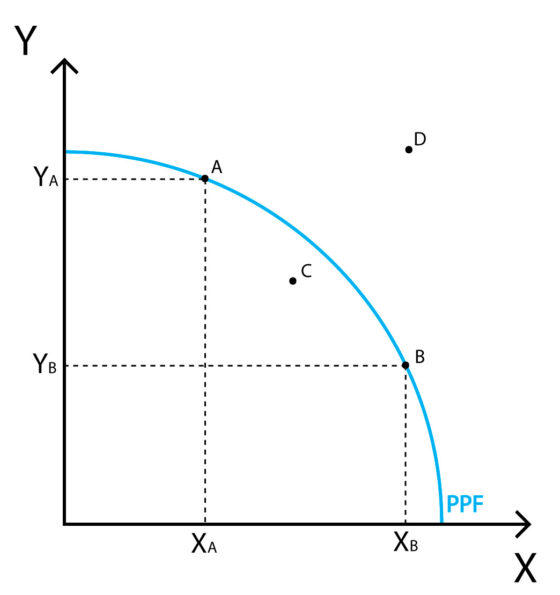
Points A/B relate to Pareto Optimal production, C is possible yet not Pareto, as production is less than it could be. D is an unachievable level of production given our input constraints.
Now we get the concept, let’s solve this problem for the 60 million people in the UK whilst also price all their goods and services accordingly. This begins our next optimisation, which focuses on how markets (attempt) to optimise the allocation of resources to be Pareto Optimal.
The Invisible Hand
Adam Smith (certified GOAT) described the optimiser of the market as “The Invisible Hand” which pushes us toward a Pareto Optimal state. Mathematically, given certain (almost ludicrous) assumptions, markets will settle into these optima. To understand the proof with some very pretty graphs check this blog. As a sketch, the proof shows that a market with rational agents will reach an “equilibrium” which is pareto optimal and anything less is a contradiction, but let’s imagine a situation where we currently are not - and how this would change.
So let’s say Mr. Burns has got in the business of making premium sneakers - Air Jordans. He buys both unbranded shoes and logo patches, then sticks ’em together. He want to work out how many shoes to make - in econ we call this the production maximisation problem. The price of Jordans is set by the market, so really as a producer his focus should be on reducing the cost to a specific amount.
He has two things to control: labour and quantity of inputs (unbranded shoes/badges). If labour allows, he could buy more inputs - to make more Jordans. As a producer he may see an opportunity to refine his technology and require less labour for the same number of Jordans. He makes this decision to reduce costs and improve profits. This is a Pareto improvement, it’s an action he can take with no reduction to any other variables - it’s like free energy in a system. Behavioural economists would call this a dominant strategy for him to take.
In a perfect market, where there’s low barriers to entry and perfect information, eventually somebody is going to copy him. And the difference is, these new entrants will tolerate a lower profit margin than Mr Burns and so set their products at a lower price. This is a Pareto improvement for them, as they’ve gone from making no profit, to making some profit, whilst hopefully not to the detriment of Burns. This breaks the behavioural economics conventions as we’ve added new players who are not encumbered by previous positions (this is how markets dodge falling into a Nash Equilibrium).
Now let’s consider the consumer, Bart Simpson and his optimisation. Bart normally goes to the Kwik-E-Mart (where Mr.Burns sells his Jordans) but now finds the same product for cheaper online. Any guess what he’ll do? Stop buying them from the Kwik-E-Mart. Bart is going to buy the same product for less, taking another Pareto improvement. This is great for the customer (Bart), he now has more money to spend on all his other preferences. It’s winning all around.
Now we look at the large picture - let’s imagine if the price could change. The demand for Mr. Burns’ product is reducing as he can’t attract customers at the previous price (and profit margin). Also since his technology discovery, loads of new players are selling Air Jordans, as the barrier to entry has lowered.
As there is more supply of the product and everybody is selling at a lower price, in order to stay profitable, Burns must also reduce his prices, this is another Pareto improvement (as our total profits will go up again). The market will continue to make these improvements- until no single agent can make one - at this point we’ll fundamentally be at a Pareto optimal market. In this utopia, products are valued close to their true values, and individuals preferences are satisfied!
The Characteristics to Care about
So how does the market achieve its final optimal state? Well it’s a collective decision of every agent in the system (or is meant to be). Every single action is a step in the optimisation process and thus, each step needs to be fully informed. Economists call this having perfect information and when this assumption is void, things get pretty sour (a great example of this is the market for Lemons). Unfortunately this applies to many places where society fails today - e.g insurance and health markets.
So do markets really supersede culture, as the dominant quantity to optimise? Well most things, which sapiens cared about through culture (e.g information), can now be considered intellectual property or commodities in the market. In the above example, we saw how developing our knowledge of Jordans production allowed producers to lower their costs and create more profit. So the market is able to direct what information we seek - we incentive specific cultural evolution by adding a profit incentive for refining these memes. This profit incentive also helps allocate people to the correct problem, for example the cost of cancer in the UK is £18 billion, and as such many companies appreciate the large profit in solving a problem of such magnitude and investment into biotech companies to solve this problem.
As the market churns in the background, a problem continues to be that labour is expensive - and more importantly we can’t reduce the cost without being unethical. As such, there is a massive incentive to reduce the need for labour, be it in the invention of the steam engine or in electricity to transport work efficiently. However labour is hard to replace, as it is able to do highly dexterous and intelligent tasks. Thus we began pushing engineering and computing which can help automate these tasks.
And so as computing shows promise the market focuses on pushing costs down and encouraging innovation. One of economists’ favourite examples of this is Moore’s law, which roughly suggests compute power doubles every 2 years. Eventually this leads to compute being so readily available that another form of optimisation could begin - in 2008 Geoffrey Hinton demonstrated how we could use stochastic gradient descent to train neural networks to complete human level vision tasks
Agents/BackProp
2020 - Dunno
“Agent” is a deliberately ambiguous term to describe anything which takes “actions”. Depending on the layer of abstraction this can be a physical gate in a circuit, all the way up to you - the human (or language model) reading this. When we talk about agents (such as MuZero) we’re talking about lines of code which to some capacity take inputs of an environment (e.g board of Chess/Go/Shogi) and outputs the next best move.
Currently our smartest agents are built from neural networks, a formulation of computing inspired by how neurons are wired in biological intelligence. A network consists of many densely connected neurons each with their own associated weight. These weights $W$, varying between 0 and 1, affect the output of each neuron and as such, the network. The weights of the network, and the way we’ve organised the neurons (topology), are optimised to fit our agents’ needs. Mathematically we can consider networks as universal function approximators, meaning we can encode any function into a neural network, that means for whatever $x$ and $y$, we can find a neural network $f$ with weights $W$ such that $y=f(x,W)$.
Agents start with random weights and a fixed topology, effectively “dumb” (tabula rasa to the philosophy efficonados). It is through training and exposure to data that the agent/network will learn how to behave. Thinking back to our original optimiser framework, the fixed system is the environment and an agent, where the environment can vaguely be “whatever we care to learn”. Whilst the weights are the configuration of the systems we want to optimise. The environment could be as mundane as a dataset for house sizes/prices to an interactive Atari game with a high score to beat. We let agents to interact with the dataset/environment and depending on their outcomes (e.g score on the game or correct house price), we change the weights of the neurons.

The very act of training a neural network is the optimisation. We search through the different values of each neuron such that the network performs better on a task. To do this search effectively we use a process called back propagation.
Let’s freeze the weights of the network for a second. We have an input $x$, for example a game board or a series of quantities representing a house (number floors, number bathrooms, etc) and a label $y$, which is the expected answer (score / house price). We feed $x$ through our network and get our predicted answer $y’=f(x)$. The loss is the difference between $y’$ and $y$, which depending on what $y$ is could simply be a numerical difference ($y’-y$) to something more complex - mathematicians care that this a differentiable metric. It is this loss $l$, which is the value we optimise (e.g minimise) in this section.
We fixed the weights to calculate the loss, now let’s try updating them to reduce it. Backprop calculates the gradients of error with respect to our weights at time $t$, $dl/dW_t$. This value gives us an understanding of the surface of loss to weights, and if we travel down this slope (given by the gradient) we can reduce our error, The update rule looks something like this:
$$W_{t+1} = W_{t} - \alpha \frac{dl}{dW_t}$$
We apply this update rule multiple times, with tonnes of samples $(x,y)$ and using a sufficiently small steps $\alpha$, we can learn a general way to reduce the loss. To add some nomenclature we calculate the loss in a “forward” step of the network and then the gradients in a single “backwards” step. The gradients can be considered the back propagation of the loss through the network. We also calculate all the weights at the same time, hence we use a capital $W$ to signify its a matrix.
To recap and use our existing framework, our system is the agent and the environment with the weights of the agents neural network being our configuration to optimise. We optimise these configurations to have the lowest loss possible.
So how does this algorithm relate to self driving cars, talking chatbots and world class Go players? Well in each case, we’re simply training agents with labelled data. For self-driving cars we take thousands of hours of footage and ask networks to learn to correctly predict how humans would act. For talking chat-bots we scrape thousands of lines of text, blanking out words and ask neural networks to correctly predict the blank spaces (this falls back onto what linguists call The distributional hypothesis). Finally for world class Go players, networks play against themselves thousands of times, learning from the final win/loss if moves were useful.
The largest factor influencing these networks is the structure/topology which leverage important characteristics of each task. For self-driving cars, convolutional layers, inspired by the visual cortex in animals, leverage a specific structure local symmetry of connected neurons to perform exceptionally well on visual tasks. For chatbots, attention based mechanisms, where inputs attend to others within a long sequence, have allowed language models to mimicked how we too consume text. Finally for games like Go, agents have leveraged the understanding that all the information required to win is encoded in your current or local state (we call this the markov-chain assumption).
Also backprop doesn’t refer to a single algorithm but a class of gradient based methods, which optimise along an error signal and through a differentiable network. In honesty, it’s still unclear which optimiser is the best for all, however it is clear that there is no one optimiser to rule them all.
Looking Forward
So is backprop the path to full blown artificial general intelligence (AGI)? I think our most promising mechanism to reach AGI is iterative amplification. Amplification is when we set agents the tasks of building smarter agents, who in turn build even smarter agents. For a full treatment of how this works (and how to mitigate any associated risk) check out Paul Christiano’s blog.
This a compelling approach, as it falls into our world view - where we optimise until we find a new more efficient optimiser. Let’s look at the evidence that this works. Currently as researchers we push machine learning forward under four approaches:
- New architectures (topologies of a network)
- Collect larger and more interesting datasets (better environments)
- Make more efficient implementations of current algorithms (efficient compute)
- New algorithms for training (better optimisers)
Just as we apply ourselves to create better versions of these - can the same be done with agents? Already we use genetic algorithms (like in the replicators) to discover optimal architectures. If anything we’d hope to do this using our slew of optimisers at even larger scales. The problem is that unlike our previous optimisers, it is unclear what the system, configuration, objectives are for each task. More interestingly for our understanding is what can we learn from seeing how previous optimisation tasks worked? Here are some key takeaways from our previous sections:
Optimisers create positive improvement loops
Culture created language to allow for faster cultural optimisation, markets create more resources for even more resource optimisation, and genes influence their environment and resources to support even more variants - our fastest optimisers have this confounding factor which makes each iteration even faster or impactful than the prior. These are non-linear relations where the rate of optimisation increases with time. It is unclear if when agents create smarter agents, that this will be a linear increase in intelligence (we don’t even have a set scale), yet for this to work, we must find a mechanism for increasing intelligence that leverages the current available intelligence.
New optimisers turn up quicker and quicker
Look at the interval between optimiser handovers, entropy took 10 billion years to create genes, 4 billion years later culture appears, and takes only a mere 100,000 years to form markets. Under markets and their pressures, it’s 3000 years to make agents. The gap between handovers is reducing logarithmically, this fits well with iterative amplification - which would allow agents to continuously introduce new optimisers for the new tasks they determine need to be optimised.
Strong optimisers, can go more wrong
Entropy optimisation rarely goes wrong, and in those situations we get strange behaviour such as spin ice - which overtime is self correcting. When genes incorrectly optimise we get cancer cells - which whilst dangerous to individual genes are limited to the carrier. Culture can create harmful memes - the worst (such as nukes) are cause for existential risk not only to the optimisation of culture but also life. Markets when incorrectly modelled without perfect information can lead to wasteful allocation of resources can lead to wars, eradicating trust for markets, cultures and life. Each optimisation can go wrong - and with it we must appreciate that the impact of misaligned agents will be even more catastrophic.
Optimisers get faster at completing more difficult tasks
This statement is much harder to quantify so let’s just outline a sketch. Entropy evolution is a tediously slow process, with irreversible processes taking thousands of years to create simple structure. Genes on the other hand replicate exceptionally quickly making even more complex structures. Next, if we compare genetic evolution with cultural evolution, we find the largest difference is that genes use survival to evaluate fitness whilst memes require other people to imitate them to evaluate fitness. Thus, the optimisation step for genes is once a generation whilst for memes it is almost instantaneous. Equally by considering markets, the true values of a resource propagate almost instantaneously, to the point that market equilibrium shift so quickly that government intervention is required at times.
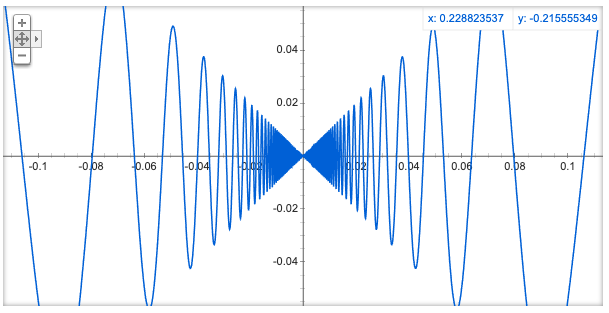
The rigorous way to evaluate this is to consider how big the search space is which each optimiser must travel through. Further considerations also include the nature of the surface, in terms of continuity and shape. For example, both surfaces shown below have minimum at the same point - however in the oscillatory example, its much harder to find the minimum.